–õ—é–Ī–ĺ–Ņ–ł—ā–Ĺ–ĺ –∑–į —á–ł—Ā–Ľ–į—ā–į –ĺ—ā —Ä–Ķ–ī–ł—Ü–į—ā–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł
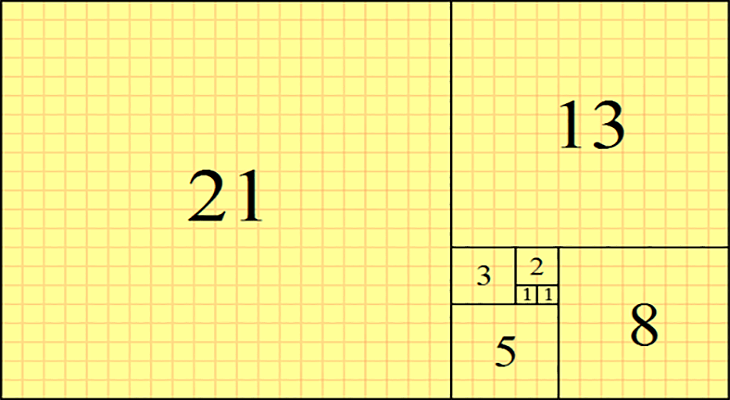
–°–Ĺ–ł–ľ–ļ–į: –ß–ł—Ā–Ľ–į—ā–į –ĺ—ā —Ä–Ķ–ī–ł—Ü–į—ā–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł
–ß–ł—Ā–Ľ–į—ā–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į –ĺ–Ī—Ä–į–∑—É–≤–į—ā —Ä–Ķ–ī–ł—Ü–į, –ļ–ĺ—Ź—ā–ĺ —Ā–Ķ –ī–Ķ—Ą–ł–Ĺ–ł—Ä–į —Ä–Ķ–ļ—É—Ä—Ā–ł–≤–Ĺ–ĺ –Ņ–ĺ —Ā–Ľ–Ķ–ī–Ĺ–ł—Ź –Ĺ–į—á–ł–Ĺ:
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2)
–ó–į–Ņ–ĺ—á–≤–į —Ā–Ķ —Ā 0 –ł 1, –į –≤—Ā–Ķ–ļ–ł —Ā–Ľ–Ķ–ī–≤–į—Č —á–Ľ–Ķ–Ĺ –Ĺ–į —Ä–Ķ–ī–ł—Ü–į—ā–į —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į –ļ–į—ā–ĺ —Ā—É–ľ–į –Ĺ–į –Ņ—Ä–Ķ–ī—Ö–ĺ–ī–Ĺ–ł—ā–Ķ –ī–≤–į.
–ü—ä—Ä–≤–ł—ā–Ķ —á–ł—Ā–Ľ–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł —Ā–į:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
–ė—ā–į–Ľ–ł–į–Ĺ—Ā–ļ–ł—Ź—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –§–ł–Ī–ĺ–Ĺ–į—á–ł –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į –Ņ—Ä–Ķ–∑ 1202 –≥. —Ä–Ķ–ī–ł—Ü–į –ĺ—ā —á–ł—Ā–Ľ–į, –≤—Ā—Ź–ļ–ĺ –ĺ—ā –ļ–ĺ–ł—ā–ĺ —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į –ļ–į—ā–ĺ —Ā—É–ľ–į –ĺ—ā –Ņ—Ä–Ķ–ī—Ö–ĺ–ī–Ĺ–ł—ā–Ķ –ī–≤–Ķ, –ļ–į—ā–ĺ –Ņ—ä—Ä–≤–ł—ā–Ķ –ī–≤–Ķ —á–ł—Ā–Ľ–į —Ā–į 0 –ł 1: 0, 1, 1, 2, 3, 5, 8, 13, 21,… –Ę–ĺ–Ļ –Ķ –Ĺ–į—É—á–ł–Ľ –∑–į —ā–į–∑–ł —Ä–Ķ–ī–ł—Ü–į –ĺ—ā —á–ł—Ā–Ľ–į –Ņ–ĺ –≤—Ä–Ķ–ľ–Ķ –Ĺ–į –Ņ—ä—ā–Ķ—ą–Ķ—Ā—ā–≤–ł—Ź—ā–į —Ā–ł –≤ —Ā—ā—Ä–į–Ĺ–ł—ā–Ķ –ĺ—ā —ā–ĺ–≥–į–≤–į—ą–Ĺ–ł—Ź –ė–∑—ā–ĺ–ļ –ł —Ä–Ķ–ī–ł—Ü–į—ā–į –Ķ –Ī–ł–Ľ–į –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į –Ĺ–į –Ĺ–Ķ–≥–ĺ–≤–ĺ –ł–ľ–Ķ, –∑–į—Č–ĺ—ā–ĺ —Ź –Ķ –Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–ł–∑–ł—Ä–į–Ľ.
–ě–ļ–į–∑–≤–į —Ā–Ķ, —á–Ķ –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ņ–ĺ-–≥–ĺ–Ľ–Ķ–ľ–ł —Ā–į —á–ł—Ā–Ľ–į—ā–į –ĺ—ā —Ä–Ķ–ī–ł—Ü–į—ā–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł, —ā–ĺ–Ľ–ļ–ĺ–≤–į –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ī–≤–Ķ—ā–Ķ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł —á–ł—Ā–Ľ–į —Ā–Ķ –Ņ—Ä–ł–Ī–Ľ–ł–∂–į–≤–į –ī–ĺ '–∑–Ľ–į—ā–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ' –ł –Ņ—Ä–ł –≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ –Ņ—Ä–Ķ—Ö–ĺ–ī (–Ņ—Ä–ł –Ī–Ķ–∑–ļ—Ä–į–Ķ–Ĺ –Ī—Ä–ĺ–Ļ —á–ł—Ā–Ľ–į –≤ —Ä–Ķ–ī–ł—Ü–į—ā–į) —Ā—ā–į–≤–į —Ä–į–≤–Ĺ–ĺ –Ĺ–į '–∑–Ľ–į—ā–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ'.
–Ě–į —Ā–Ĺ–ł–ľ–ļ–į—ā–į: –ö–≤–į–ī—Ä–į—ā–ł, —á–ł–ł—ā–ĺ —Ā—ā—Ä–į–Ĺ–ł—á–Ĺ–ł –ī—ä–Ľ–∂–ł–Ĺ–ł —Ā–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł —á–ł—Ā–Ľ–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł